Modern Portfolio - Practical
Let's get into detailed mechanics of the Efficiency frontier and Modern Portfolio Theory of Harry Markowitz. Take a time out and slowly understand the following.
Imagine you're standing at the edge of a vast, uncharted territory, armed with a map and a compass. You're about to embark on a journey, but the terrain is treacherous and the path is unclear.
This is the world of investing, and the map you hold is the Efficient Frontier.
The Efficient Frontier is a concept in finance that helps investors navigate the complex relation of risk and return. It's like a map that shows you the optimal portfolios that offer the highest expected return for a given level of risk, or the lowest risk for a given level of expected return.
To better understand the Efficient Frontier, let's break it down into its key components.
Risk and Return
Risk and return are the two sides of the same coin in investing.
Generally, the higher the potential return, the higher the risk. Conversely, lower risk investments typically offer lower returns.
The Efficient Frontier is typically represented as a curve on a graph, with the x-axis representing risk (measured by standard deviation) and the y-axis representing return (measured by compound annual growth rate).
Each point on the curve represents a different portfolio, and the curve itself represents the set of optimal portfolios.
The Efficient Frontier is constructed using mathematical models and optimization methods. It identifies the optimal portfolio combinations that offer either the highest expected return for a specific risk level or the lowest risk for a particular expected return.
To construct the Efficient Frontier, you need to consider a mix of risky assets (e.g., stocks) and a risk-free asset (e.g., government bonds). The risk-free asset provides a baseline return with zero risk.
The Efficient Frontier starts at this point and extends upward as you add more risky assets.
Portfolio Optimization Steps:
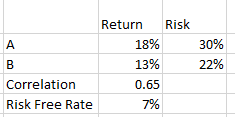
1. Define the risk-free rate and the expected returns and standard deviations of the risky assets.
2. Calculate the expected return and standard deviation of each possible portfolio.
3. Identify the portfolio with the highest expected return for each level of risk.
4. Plot these portfolios on a graph to create the Efficient Frontier.
Something like the following:
Where the variables are as under:
Practical Applications
The Efficient Frontier is not just a theoretical concept; it has practical applications in portfolio management. By analyzing the risk and return of different portfolios, you can visualize the construction of the Efficient Frontier and identify the optimal portfolio for your specific risk tolerance.
For example, if you're a risk-averse investor, you may choose a portfolio that lies to the left of the Tangency Portfolio, where the risk is lower but the expected return is also lower.
On the other hand, if you're a risk-seeking investor, you may choose a portfolio that lies to the right of the Tangency Portfolio, where the risk is higher but the expected return is also higher.
The Efficient Frontier is a fundamental concept in finance, serving as a guiding principle for investors seeking to navigate the delicate balance between risk and return within their portfolios.
By understanding the Efficient Frontier and its practical applications, you can make more informed investment decisions and maximize your returns while minimizing your risk.
The Capital Market Line
The Capital Market Line (CML) is a tangent line that touches the Modern Portfolio Theory curve at the risk-free rate and extends into the set of optimal portfolios. The CML represents the optimal portfolio for an investor with a certain risk tolerance.
The Tangency Portfolio offers the highest return for a given level of risk and is often considered the optimal portfolio for an investor with a specific risk tolerance.
By analyzing the risk and return of different portfolios, you can visualize the construction of the Modern Portfolio Theory curve and identify the optimal portfolio for your specific risk tolerance.
By understanding the Modern Portfolio Theory and its practical applications, you can make more informed investment decisions and maximize your returns while minimizing your risk.
Thanks for tuning in.
Love you all.